THE UNITED REPUBLIC OF TANZANIA NATIONAL EXAMINATIONS COUNCIL OF TANZANIA
CERTIFICATE OF SECONDARY EDUCATION EXAMINATION
041BASIC MATHEMATICS
(For Both School and Private Candidates)
Time: 3 HoursYear: 2024
Instructions
- This paper consists of sections A and B with a total of fourteen (14) questions.
- Answer all questions.
- Each question in section A carries six (06) marks while each question in section B carries ten (10) marks.
- All necessary working and answers for each question must be shown clearly.
- NECTA mathematical tables and non-programmable calculator may be used.
- All communication devices and any unauthorised materials are not allowed in the examination room.
- Write your Examination Number on every page of your answer booklet(s).
SECTION A (60 Marks)
Answer all questions in this section.
1. (a) Equal squares which are as large as possible are drawn on a rectangular board measuring 54 cm by 78 cm. Find the size of each square.
View Ans
(b) In a class of 40 students, 17 students are boys and the rest are girls. Determine;
(i) the percentage of girls and boys.
(ii) the number of boys in decimal.
View Ans
2. (a) Express 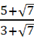 in the form
in the form 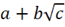 , where a, b, and c are integers.
, where a, b, and c are integers.
View Ans
(b) A line is defined by a logarithmic equation 3log3 x+4 =log324. Without using a mathematical table or calculator, find the value of x. ,
View Ans
3. (a) In a school of 100 students, 45 students prefer Music subject, 40 students prefer Theatre Arts subject and 5 students prefer both subjects. Find the number of students who prefer none of the two subjects by using formula.
View Ans
(b) The following table shows the number of tables in twenty offices from a certain company:
| Number of Tables | Number of Offices |
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
| 4 | 2 |
| 5 | 1 |
| 6 | 2 |
If one offices picked randomly, find the probability that the office has;
(i) two tables.
(ii) at least five tables
View Ans
4. (a) A quadrilateral has the vertices, A (6,-4), B (8,4), P (6,1) and Q (7,5). Determine whether or not AB is parallel to PQ.
View Ans
(b) The points P and Q have position vectors a and b, respectively. If a = 2 f —7 j and 2a + 3b =13i —2 j , find the components of vector b
View Ans
5. (a) The area of a regular six-sided plot of .a land inscribed in a circular track of radius r is 720 m2. Find the value of r by rounding off the answer to the nearest:
(i) tens.
(ii) tenths.
View Ans
(b) A firm reserved two triangular plots for the construction of more offices as shown in the following diagram:
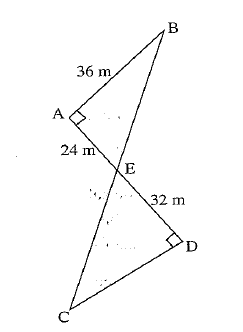
(i) Prove that the triangles AEB and CDE are similar.
(ii) Using similarity properties, find the length of CD in metres.
View Ans
6. (a) On one rainy day, it was observed that 850 millilitres of water were collected in a tank every minute. If it rained continuously from 8:10 a.m. to 11:52 a.m., calculate in litres, the amount of water collected.
View Ans
(b) The time t in seconds that is used by Mary to go back home from school varies inversely with her average speed v in metres per second. She gets back home in 30 minutes at an average speed Of 10m/s
(i) Write an equation expressing t in terms of v .
(ii) If she 'Wants to get back home in 15 minutes, What will be her average speed?
View Ans
7. (a) If the sum and difference of ages of Amina and Bakari are in the ratio 5 : 4 , what would be the ratio of their respective ages?
View Ans
(b) On 1st July, 2021, a small scale trader started a business with capital in cash of 1,000,000 shillings. The trader's cash account at the end of the month was as follows:
| DR | TRADER'S CASH ACCOUNT | CR |
| Date | Particulars | Folio | Amount | Date | Particulars | Folio | Amount |
| July 1 | Capital | 1 | 1,000,000 | July 2 | Purchaies. | 2 | 700,000 |
| 3 | Sales | 3 | 500,000 | 6 | Purchases | 4 | 300,000 |
| 28 | Sales | 5 | 310,000 | 10 | Purchases | 8 | 235,000 |
|
|
|
| 15 | Rent | 10 | 110,000 |
|
|
|
| 26 | Wages | 15 | 55,000 |
|
|
|
| 31 | Balance | c/d | 410,000 |
|
|
| 1,810000 |
|
|
| 1,810,000 |
| August 1 | Balance | b/d | 410,000 |
| |
|
|
View Ans
8. An entrepreneur borrowed a loan from a bank under the condition that he is required to repay the. loan on monthly installment basis. The entrepreneur repaid 20,000, 22,000, 24,000 shillings for the first, second and third installments respectively until the loan ,was fully repaid.
(a) If the final monthly installment was 114,000 shillings, how long did the entrepreneur take to repay the whole loan?
(b) Calculate the total amount of loan borrowed.
View Ans
9. (a) By applying your knowledge of trigonometry show that 4 sin75° . = 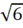 +
+ 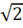
View Ans
(b) An electricity post AB is supported by two pieces of wire,AC and AD, on the top at point A and the ground at points C and D. If the length of AC is 10 m, the distance between points C and D is 4 m and the height of the post is 6 m, find the length of wire AD, leaving your answer in surd form.
View Ans
10. (a) A candidate obtained a minimum average of 53 marks in two Mathematics tests. If she scored 54 marks in the first test, what is the least possible mark she would have scored in the second test?
View Ans
(b) You are asked to make a fence for a garden using a wire which is 56 metres long. The fence should be rectangular in shape with an area of 171 square metres. What will be the dimensions of the fence enclosing the garden?
View Ans
SECTION B (40 Marks)
Answer all questions in this section.
11. (a) In the terminal examination of a certain school, the scores of students in Geography subject were grouped as shown in the following table:
| Scores | 65 - 69 | 70 - 74 | 75 - 79 | 80 - 84 | 85 - 89 | 90 - 94 | 95 - 99 |
| Cumulative Frequency | 10 | 22 | 43 | 49 | 58 | 62 | 66 |
Using the information given in the table;
(i) find the mean score correct to 2 decimal places, given an assumed mean of 77.
(ii) draw the cumulative frequency curve (ogive) of the scores.
(iii) calculate the mode of the scores correct to 3 decimal places.
View Ans
(b) In the following figure, PT is a tangent to a circle whose centre is at point 0 and the radius is 5 cm. If PC is 8 cm, find the length of PT.
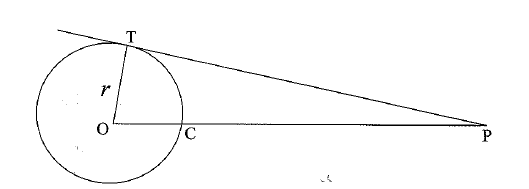
View Ans
12. (a) (i) The surface area of a sphere is 113.04 cm2. Find its diameter (Use π = 3.14).
(ii) 75.360 litres of water are poured into a cylindrical tank of inside diameter of 40 cm. Calculate the height of the water level.
View Ans
(b) Find the distance in nautical miles between each of the following pairs of points:
(i) A(18°N, 12°E) and B(65°N, 12°E).
(ii) C(31°S, 76°W) and D(22°N, 76°W).
View Ans
13. (a) Roza and Juma were asked to write the examples of a 2x 2 matrix and they came up with 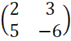 and
and 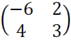 respectively.
respectively.
(i) Find the sum of twice the Roza's matrix and thrice the Juma's matrix.
(ii) Show that the difference between the determinants of these matrices is ±1.
View Ans
(b) If a farm measuring 72 m by 88 m is enlarged by a scale factor of 4, what will be the area of the enlarged farm?
View Ans
14. (a) During an inter-school quiz core petition each correct answer y was awarded a number of points x related by the function y = 3x2.
(i) How many points would a competitor collect by answering 8 questions correctly?
(ii) Find the domain and range of the inverse of the given function.
View Ans
(b) A cook wishes to mix two types of foods, I and II in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kilogram of food are given in the following table.
|
| Vitamin A | Vitamin B | Vitamin C |
| Food type I | 1 | 2 | 3 |
| Food type II | 2 | 2 | 1 |
One kilogram of Food type I costs Tsh 6,000 and one kilogram of Food type II costs Tsh. 10,000.
(i) Formulate the linear programming model to minimize the cost.
(ii) What is the minimum cost of the mixture of food?
View Ans
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256
 For Call,Sms&WhatsApp: 255769929722 / 255754805256
For Call,Sms&WhatsApp: 255769929722 / 255754805256